GIR: 3D Gaussian Inverse Rendering for Relightable Scene Factorization

Yahao Shi1*, Yanmin Wu2*, Chenming Wu3#, Xing Liu3, Chen Zhao3, Haocheng Feng3,
Jingtuo Liu3, Liangjun Zhang3 Jian Zhang2† Bin Zhou1† Errui Ding3 Jingdong Wang3
1Beihang University, 2Peking University, 3Baidu VIS
*Equal contribution, #Project lead, †Corresponding authors
Paper arXiv Code

Real-Time rendering and relighting achieved by our GIR.

Abstract

This paper presents GIR, a 3D Gaussian Inverse Rendering method for relightable scene factorization. Compared to existing methods leveraging discrete meshes or neural implicit fields for inverse rendering, our method utilizes 3D Gaussians to estimate the material properties, illumination, and geometry of an object from multi-view images. Our study is motivated by the evidence showing that 3D Gaussian is a more promising backbone than neural fields in terms of performance, versatility, and efficiency. In this paper, we aim to answer the question: "How can 3D Gaussian be applied to improve the performance of inverse rendering?" To address the complexity of estimating normals based on discrete and often in-homogeneous distributed 3D Gaussian representations, we proposed an efficient self-regularization method that facilitates the modeling of surface normals without the need for additional supervision. To reconstruct indirect illumination, we propose an approach that simulates ray tracing. Extensive experiments demonstrate our proposed GIR's superior performance over existing methods across multiple tasks on a variety of widely used datasets in inverse rendering. This substantiates its efficacy and broad applicability, highlighting its potential as an influential tool in relighting and reconstruction.

Method

Pipeline of GIR

In this paper, we answer this question by introducing GIR, a novel inverse rendering framework based on 3DGS that estimates material properties, geometry, and illumination from multi-view images in high fidelity. We address the challenge of accurately modeling surface normals in 3D Gaussian representations. The complexity arises from the discrete and often in-homogeneous distribution of these Gaussians. This makes the learning of accurate normals nontrivial without the use of regularization. Moreover, the normal regularization methods designed for learning implicit Signed Distance Functions (SDF), such as the one used in NeuS cannot be applied in this context. We thus propose an efficient self-regularization method that ensures the shortest axis of each visible 3D Gaussian forms an obtuse angle with the camera's principal axis. Furthermore, we propose an approach for indirect illumination reconstruction that is suited for 3D Gaussian representation. Extensive experimental analyses have demonstrated that our proposed approach significantly outperforms existing methods on various datasets across multiple tasks.

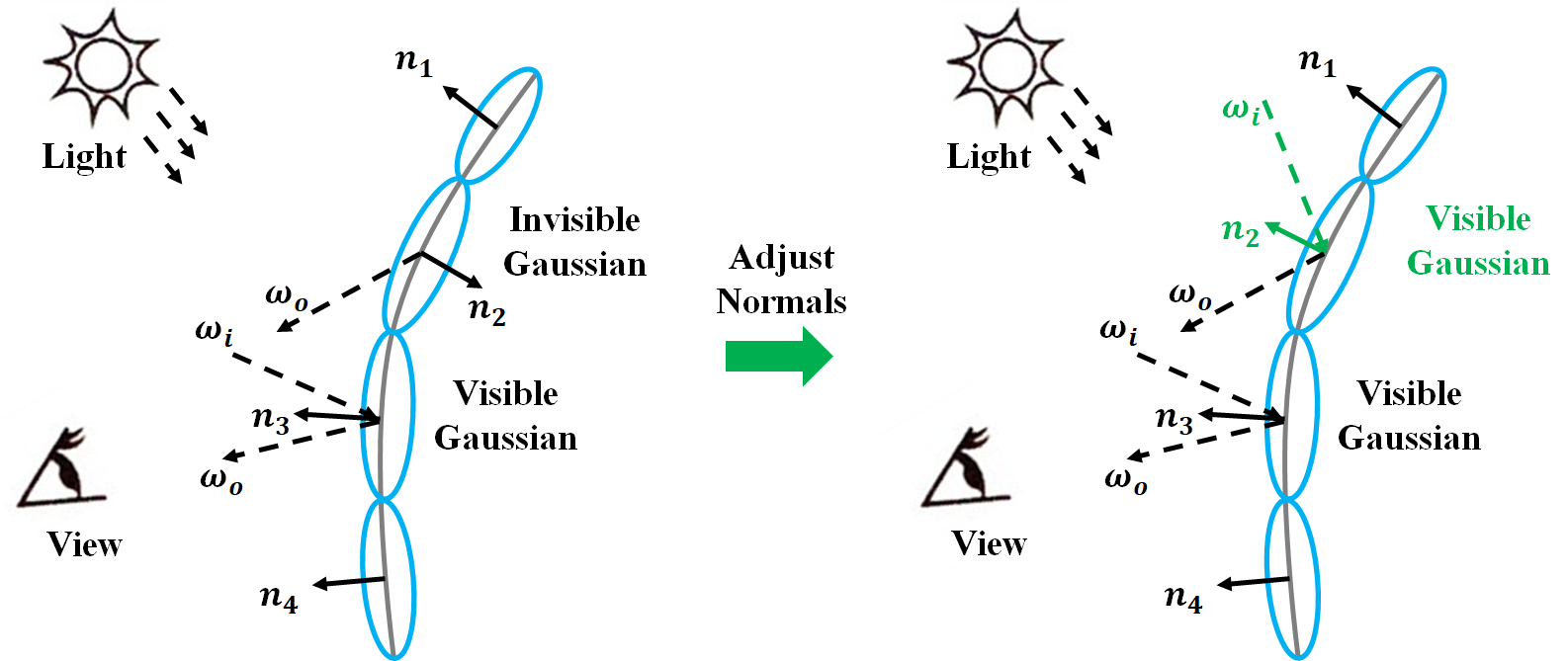
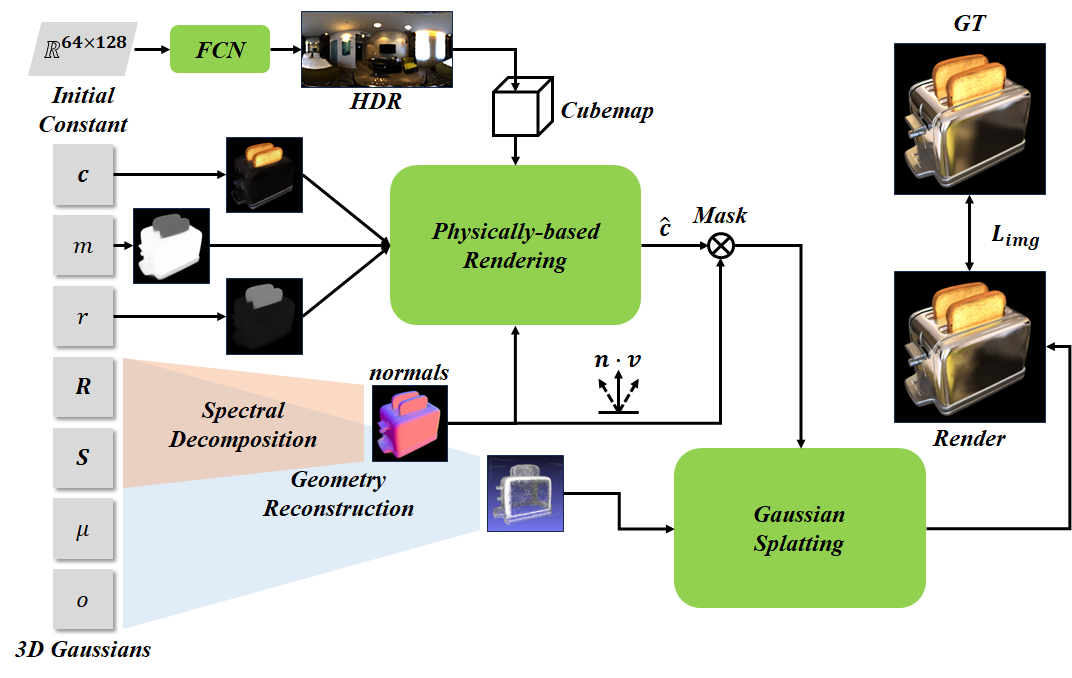
Interpolate start reference image Interpolate start reference image

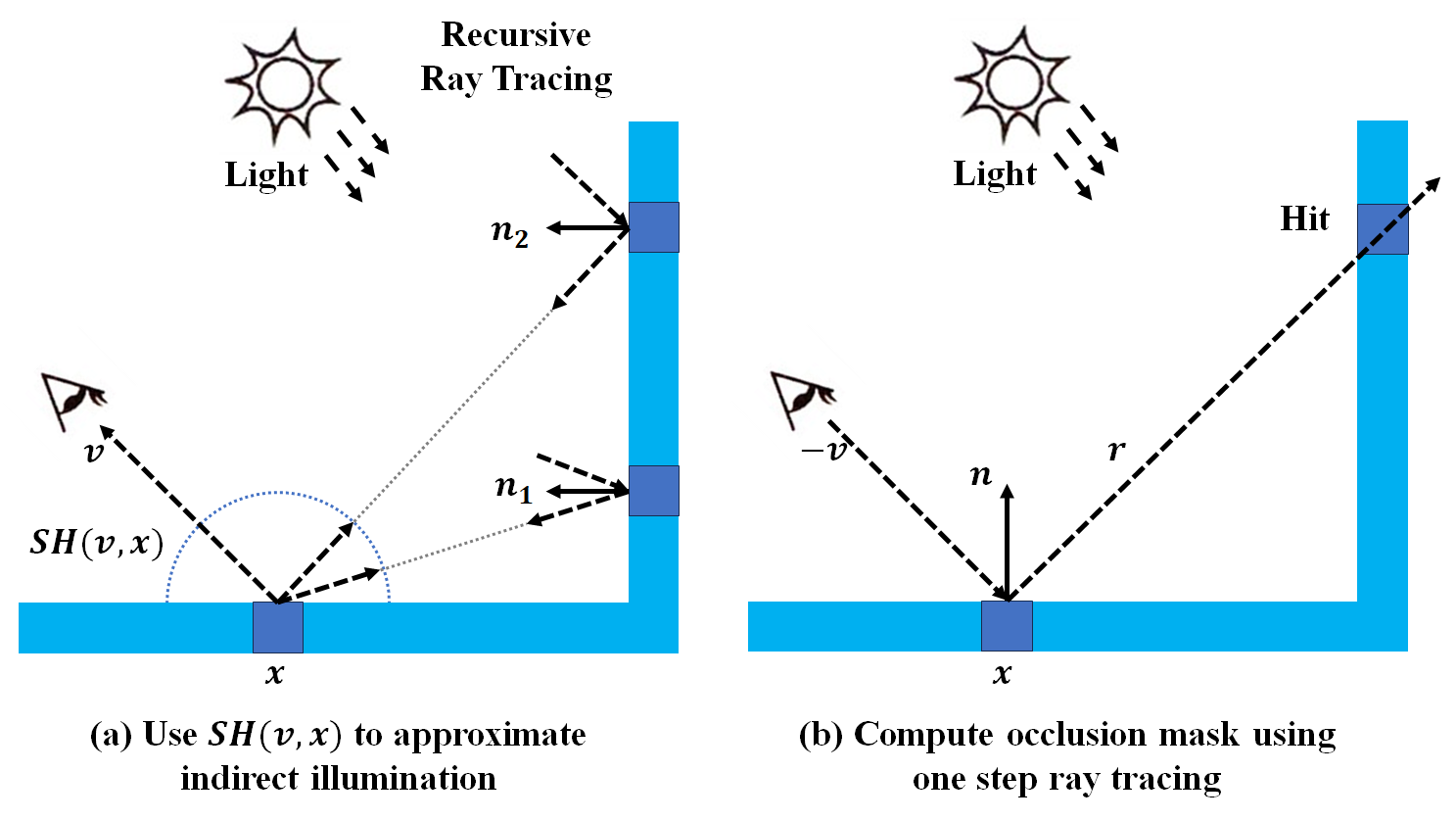
Normal Estimation

Gaussians present on the surface and observed from the viewpoint should be visible. Any Gaussian that is not visible, as determined by $\mathbf{n} \cdot \mathbf{v} \leq 0$, does not contribute to color calculations. Therefore, the normal direction of these invisible Gaussians needs to be modified in order to reconstruct the desired image.

Interpolate start reference image.

Indirect Illumination

The illustration of our indirect illumination reconstruction: Instead of employing recursive ray tracing, we utilize spherical harmonic coefficients to encode the view direction, enabling the simulation of indirect illumination.

Interpolate start reference image.

BibTeX

@article{shi2023gir,
  author    = {Shi, Yahao and Wu, Yanmin and Wu, Chenming and Liu, Xing and Zhao, Chen and Feng, Haocheng and Liu, Jingtuo and Zhang, Liangjun and Zhang, Jian and Zhou, Bin and Ding, Errui and Wang, Jingdong},
  title     = {GIR: 3D Gaussian Inverse Rendering for Relightable Scene Factorization},
  journal   = {Arxiv},
  year      = {2023},
  eprint    = {2312.05133},
}